考虑模型复杂度:在验证过程中,需要平衡模型的复杂度与性能。过于复杂的模型可能会导致过拟合,而过于简单的模型可能无法捕捉数据中的重要特征。多次验证:为了提高结果的可靠性,可以进行多次验证并取平均值,尤其是在数据集较小的情况下。结论模型验证是机器学习流程中不可或缺的一部分。通过合理的验证方法,我们可以确保模型的性能和可靠性,从而在实际应用中取得更好的效果。在进行模型验证时,务必注意数据的划分、评估指标的选择以及模型复杂度的控制,以确保验证结果的准确性和有效性。这样可以多次评估模型性能,减少偶然性。奉贤区正规验证模型供应
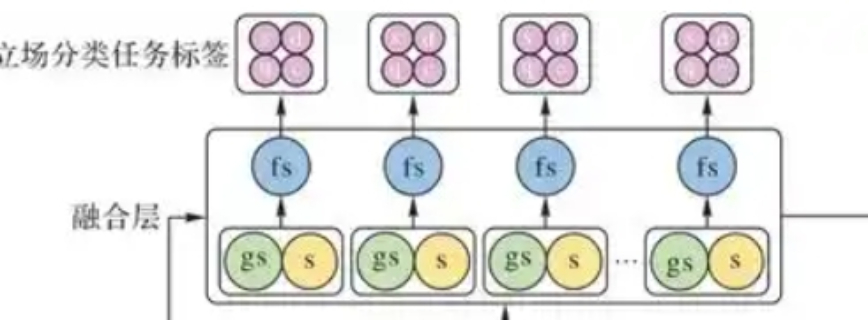
指标数目一般要求因子的指标数目至少为3个。在探索性研究或者设计问卷的初期,因子指标的数目可以适当多一些,预试结果可以根据需要删除不好的指标。当少于3个或者只有1个(因子本身是显变量的时候,如收入)的时候,有专门的处理办法。数据类型绝大部分结构方程模型是基于定距、定比、定序数据计算的。但是软件(如Mplus)可以处理定类数据。数据要求要有足够的变异量,相关系数才能显而易见。如样本中的数学成绩非常接近(如都是95分左右),则数学成绩差异大部分是测量误差引起的,则数学成绩与其它变量之间的相关就不***。奉贤区正规验证模型供应数据预处理:包括数据清洗、特征选择、特征缩放等,确保数据质量。
模型检测的基本思想是用状态迁移系统(S)表示系统的行为,用模态逻辑公式(F)描述系统的性质。这样“系统是否具有所期望的性质”就转化为数学问题“状态迁移系统S是否是公式F的一个模型”,用公式表示为S╞F。对有穷状态系统,这个问题是可判定的,即可以用计算机程序在有限时间内自动确定。模型检测已被应用于计算机硬件、通信协议、控制系统、安全认证协议等方面的分析与验证中,取得了令人瞩目的成功,并从学术界辐射到了产业界。
结构方程模型是基于变量的协方差矩阵来分析变量之间关系的一种统计方法,是多元数据分析的重要工具。很多心理、教育、社会等概念,均难以直接准确测量,这种变量称为潜变量(latent variable),如智力、学习动机、家庭社会经济地位等等。因此只能用一些外显指标(observable indicators),去间接测量这些潜变量。传统的统计方法不能有效处理这些潜变量,而结构方程模型则能同时处理潜变量及其指标。传统的线性回归分析容许因变量存在测量误差,但是要假设自变量是没有误差的。使用验证集评估模型的性能,常用的评估指标包括准确率、召回率、F1分数、均方误差(MSE)、均方根误差。
性能指标:根据任务的不同,选择合适的性能指标进行评估。例如:分类任务:准确率、精确率、召回率、F1-score、ROC曲线和AUC值等。回归任务:均方误差(MSE)、均***误差(MAE)、R²等。学习曲线:绘制学习曲线可以帮助理解模型在不同训练集大小下的表现,帮助判断模型是否过拟合或欠拟合。超参数调优:使用网格搜索(Grid Search)或随机搜索(Random Search)等方法对模型的超参数进行调优,以找到比较好参数组合。模型比较:将不同模型的性能进行比较,选择表现比较好的模型。外部验证:如果可能,使用**的外部数据集对模型进行验证,以评估其在真实场景中的表现。回归任务:均方误差(MSE)、误差(MAE)、R²等。杨浦区智能验证模型供应
根据需要调整模型的参数和结构,以提高模型在训练集上的性能。奉贤区正规验证模型供应
验证模型是机器学习和统计建模中的一个重要步骤,旨在评估模型的性能和泛化能力。以下是一些常见的模型验证方法:训练集和测试集划分:将数据集分为训练集和测试集,通常按70%/30%或80%/20%的比例划分。模型在训练集上进行训练,然后在测试集上评估性能。交叉验证:K折交叉验证:将数据集分为K个子集,模型在K-1个子集上训练,并在剩下的一个子集上测试。这个过程重复K次,每次选择不同的子集作为测试集,***取平均性能指标。留一交叉验证(LOOCV):每次只留一个样本作为测试集,其余样本作为训练集,适用于小数据集。奉贤区正规验证模型供应
上海优服优科模型科技有限公司是一家有着先进的发展理念,先进的管理经验,在发展过程中不断完善自己,要求自己,不断创新,时刻准备着迎接更多挑战的活力公司,在上海市等地区的商务服务中汇聚了大量的人脉以及客户资源,在业界也收获了很多良好的评价,这些都源自于自身的努力和大家共同进步的结果,这些评价对我们而言是最好的前进动力,也促使我们在以后的道路上保持奋发图强、一往无前的进取创新精神,努力把公司发展战略推向一个新高度,在全体员工共同努力之下,全力拼搏将共同上海优服优科模型科技供应和您一起携手走向更好的未来,创造更有价值的产品,我们将以更好的状态,更认真的态度,更饱满的精力去创造,去拼搏,去努力,让我们一起更好更快的成长!